Kurt Gödel este cel mai bine cunoscut de către matematicieni și de către publicul larg pentru teoremele sale de incompletitudine. Fizicienii, de asemenea, îi cunosc faimosul său model cosmologic, în care liniile temporale se apropie una de cealaltă într-un continuum spațiu-timp curbat, astfel încât trecutul îndepărtat și viitorul sunt unul și același. Ceea ce este mai puțin cunoscut este faptul că Gödel a schițat o versiune revizuită a argumentului ontologic tradițional al lui Anselm de Canterbury, pentru existența lui Dumnezeu.
Cum ajunge un matematician să fie implicat în chestiunea legată de Dumnezeu? Gödel a fost un mistic, a cărui cercetare matematică a ilustrat o atitudine filozofică apropiată de neo-platoniști. Din acest punct de vedere, Gödel a avut multe în comun cu teologii și filozofii medievali, precum și cu matematicienii secolului XX, care au fost pionierii teoriei computației și științelor computaționale moderne. Totuși, un motiv mai profund al contribuției lui Gödel la argumentul ontologic este acela că cele mai sofisticate versiuni ale argumentului ontologic sunt scrise astăzi în termeni de logică modală, o ramură a logicii care era familiară cărturarilor medievali și care a fost axiomatizată de către C. I. Lewis (a nu fi confundat cu C. S. Lewis sau C. Day Lewis). S-a dovedit că logica modală nu constituie numai un limbaj folositor pentru discutarea chestiunii lui Dumnezeu, dar de asemenea este un limbaj util pentru teoria argumentării, studiul a ceea ce poate sau nu poate fi dovedit cadrul sistemelor deductive matematice. Chestiunile completitudinii sistemelor matematice, a independenței axiomelor față de alte axiome, și chestiunea consistenței sistemelor matematice formale constituie toate părți ale teoriei argumentării.
Discuțiile despre teoria argumentării seamănă deseori cu un discurs despre Dumnezeu:
* Atunci când vorbești despre Dumnezeu, trebuie să discuți chestiuni ca "dacă Dumnezeu a creat Universul, atunci cine l-a creat pe Dumnezeu?" În cadrul teoriei argumentării trebuie să discuți probleme ca "dacă o propoziție este adevărată, atunci este adevărat că putem dovedi propoziția?"
* În metafizică, o persoană discută posibila existență a unor lumi ipotetice în care Dumnezeu nu există. În teoria argumentării, o persoană examinează independența unei axiome prin găsirea unor modele în cadrul cărora axioma nu funcționează.
* În metafizică, o persoană poate vorbi despre "colapsul modal", în care orice propoziție care este adevărată într-o măsură oarecare este în mod necesar adevărată. În teoria argumentării, o persoană poate vorbi despre "completitudine", în care fiecare propoziție care poate fi adăugată complet sistemului de axiome poate fi dovedită din alte axiome.
O parte din munca de pionierat a lui Kurt Gödel a arătat faptul că logica modală a filozofilor, care a fost utilizată pentru analiza argumentului ontologic pentru existența lui Dumnezeu, a fost de asemenea foarte folositoare în cadrul teoriei argumentării și în matematică.
Un scurt portret biografic
Kurt Gödel s-a născut în orașul ce se numește acum Brno, în Cehia, în anul 1906. (La vremea respectivă, orașul se numea Brünn și era parte a Imperiului Austro-Ungar.) În 1923, a intrat la Universitatea din Viena, obținându-și doctoratul în anul 1929 sub supravegherea lui Hans Hahn (1879-1934), mai bine cunoscut de matematicieni drept jumătatea teoremei Hahn-Banach. Gödel s-a alăturat Universității din Viena și a devenit membru al faimosului grup al filozofilor pozitiviști până în anul 1938. În perioada în care a făcut parte din acest cerc filosofic, gândirea sa a fost influențată enorm de lucrările lui Leibniz. Acest lucru îi va influența opinia cu privire la argumentul ontologic.
Odată cu izbucnirea celui de-al Doilea Război Mondial, Kurt Gödel a hotărât să părăsească Viena. A emigrat în Statele Unite în anul 1940 și s-a alăturat Institutului pentru Studii Avansate (Institute for Advanced Study) din Princeton în 1953 până la moartea sa în 1978.
Rolul necesității modale
Așa cum a fost menționat mai sus, cadrul obișnuit pentru discutarea argumentelor ontologice pentru existența lui Dumnezeu este constituit de contextul logicii modale. Ce este însă logica modală și de ce avem nevoie de aceasta?
Să luăm în considerare următoarea "dovadă" pentru existența lui Dumnezeu. Să numim asta argumentul din omnisciență.
* Dumnezeu este înțeles ca fiind o ființă care știe absolut totul, adică este omniscient. Dacă ceva este adevărat, Dumnezeu (real sau imaginar) ar ști asta. În mod similar, dacă ceva este fals, Dumnezeu (real sau imaginar) ar ști și asta, de asemenea. Împreună cu asta se găsește faptul că noi îl concepem pe Dumnezeu ca deținând toată înțelepciunea (rațiunea). O ființă care a creat universul, dar este irațională, nu ar putea fi numită în mod corespunzător Dumnezeu.
* Toate persoanele raționale cred în propria lor existență. Chiar dacă acestea nu există, aceasta se presupune a fi o propoziție adevărată. Popeye este conceput drept crezând în propria-i existență. Acesta pur și simplu se înșală asupra acestui fapt. Indivizii reali cred în mod corect în propria lor existență, în vreme de persoanele fictive se înșală din păcate asupra acestui lucru.
* Dacă Dumnezeu nu ar exista, atunci conform primului punct de mai sus, Dumnezeu ar ști dacă există sau nu. Însă acest lucru contrazice al doilea punct. Prin urmare, Dumnezeu trebuie să existe.
Acum, nimeni nu poate crede nici măcar pentru o clipă că acest argument va convinge pe cineva de existența lui Dumnezeu. Mai degrabă, cele expuse mai sus aparțin logicii modale naive. Ce am reușit însă să dovedim prin argumentul de mai sus, dacă nu existența lui Dumnezeu?
Argumentul îl definește pe Dumnezeu ca fiind o ființă omniscientă rațională. Matematicienii au tendința de a accepta ideea că poți defini anumiți termeni așa cum vrei. Nu există vreo pretenție că acesta este Dumnezeul iudeo-creștin, sau dumnezeul altei religii. Ar trebui să acceptăm cu toții că, indiferent dacă această ființă este numită Dumnezeu sau nu, o dovadă a existenței unei ființe omnisciente raționale nu constituie o realizare neînsemnată. Așadar, nu aceasta este problema cu acest argument.
În schimb, am putea căuta argumente despre posibilitatea ca o ființă rațională să nu creadă în propria sa existență. Descartes a emis afirmația Cogito ergo sum, iar majoritatea dintre noi acceptăm ideea că a te îndoi de propria existență ar constitui o stare mentală ciudată.
Adevărata problemă este aceea că argumentul face o presupunere care nu este prezentată în mod explicit. Acesta presupune că este posibil ca o ființă omniscientă rațională să existe, unde omnisciența include cunoașterea propriei sale existențe. Prin urmare, ceea ce argumentul pare să enunțe de fapt este că:
DACĂ este posibil ca o ființă omniscientă rațională să existe, ATUNCI în mod necesar o ființă omniscientă rațională există.
Putem scrie acest lucru folosind simbolismul logicii modale drept
 g
g
 g
g
unde g este afirmația că o ființă rațională omniscientă există. Simbolul care arată ca un magnet reprezintă implicația materială. Afirmația a b este adevărată pentru implicația materială în afara cazului în care a este adevărat, iar b este fals.
b este adevărată pentru implicația materială în afara cazului în care a este adevărat, iar b este fals.
 b este adevărată pentru implicația materială în afara cazului în care a este adevărat, iar b este fals.
b este adevărată pentru implicația materială în afara cazului în care a este adevărat, iar b este fals.
Putem scrie concluzia de mai sus și sub forma
~ g
g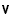
 g
g
 g
g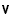
 g
g
unde 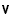 denotă o disjuncție slabă - echivalentă cu "sau/și" în limbajul obișnuit, iar ~ înseamnă negare. Alte simboluri includ a
denotă o disjuncție slabă - echivalentă cu "sau/și" în limbajul obișnuit, iar ~ înseamnă negare. Alte simboluri includ a b, "a este echivalent cu b" iar a&b, "a și b".
b, "a este echivalent cu b" iar a&b, "a și b".
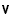 denotă o disjuncție slabă - echivalentă cu "sau/și" în limbajul obișnuit, iar ~ înseamnă negare. Alte simboluri includ a
denotă o disjuncție slabă - echivalentă cu "sau/și" în limbajul obișnuit, iar ~ înseamnă negare. Alte simboluri includ a b, "a este echivalent cu b" iar a&b, "a și b".
b, "a este echivalent cu b" iar a&b, "a și b".
Simbolurile  și
și  sunt numite simboluri modale (operatori modali) și denotă conceptul adevărului necesar (ca fiind opus contingentului sau accidentalului) și adevărul posibil. De exemplu, propoziția
sunt numite simboluri modale (operatori modali) și denotă conceptul adevărului necesar (ca fiind opus contingentului sau accidentalului) și adevărul posibil. De exemplu, propoziția
 și
și  sunt numite simboluri modale (operatori modali) și denotă conceptul adevărului necesar (ca fiind opus contingentului sau accidentalului) și adevărul posibil. De exemplu, propoziția
sunt numite simboluri modale (operatori modali) și denotă conceptul adevărului necesar (ca fiind opus contingentului sau accidentalului) și adevărul posibil. De exemplu, propoziția (există un număr prim între n și 2n pentru toate numerele întregi pozitive n)
(există un număr prim între n și 2n pentru toate numerele întregi pozitive n)
este adevărată, deoarece propoziția este demonstrabilă, iar astfel este în mod necesar adevărată. Totuși
 (un copac crește în Brooklyn)
(un copac crește în Brooklyn)
este falsă, în felul în care înțelegem noțiunile copac și Brooklyn. Faptul că un copac crește în Brooklyn constituie un adevăr contingent sau accidental, cel mai bine exprimat prin propoziția
t & ~ t
t
 t
t
unde t este afirmația că "un copac crește în Brooklyn." Nu avem nevoie de doi operatori modali, deoarece este posibil să scriem  în termeni de
în termeni de  și viceversa. Astfel
și viceversa. Astfel
 în termeni de
în termeni de  și viceversa. Astfel
și viceversa. Astfel
( a
a ~
~ ~a) & (
~a) & ( a
a ~
~ ~a)
~a)
 a
a ~
~ ~a) & (
~a) & ( a
a ~
~ ~a)
~a)
este o tautologie.
Nu trebuie să presupunem că singurele adevăruri necesare sunt cele pe care le putem dovedi. Gödel a arătat slăbiciunile acestei presupuneri cu primele două teorii ale incompletitudinii. Nici nu trebuie să presupunem că adevărul matematic și cel logic cuprind toate adevărurile necesare. Ar putea exista multe altele, de asemenea. Platon a considerat că adevărurile necesare pot și găsite, de asemenea, în estetică și etică foarte bine.
Care sunt axiomele sau postulatele logicii modale? Pe lângă postulatele obișnuite sau logica prepozițională, logica modală impune de asemenea postulate precum
 a
a a
a
pentru toate propozițiile a. Contrapoziția acestei familii de postulate este
a
 a
a

 a
a
Un alt principiu deseori folosit este și postulatul
 (a
(a  b)
b) (
( a
a
 b)
b)
care este modus ponens modal.
De asemenea, este folositor și postulatul ineluctabil
 a este adevărat când a este demonstrabil
a este adevărat când a este demonstrabil
adică, a este el însuși un postulat sau o teoremă.
Aceste postulate reprezintă nucleul comun al logicii modale. Două postulate adiționale sunt deseori oferite pentru a conferi o soliditate suplimentară. Primul dintre acestea este
 a
a

 a
a
iar al doilea este
 a
a

 a
a
Împreună, aceste două postulate susțin că statutul modal al unei propoziții este un adevăr necesar. Principiul conform căruia statutul modal al unei propoziții este un adevăr necesar este numit postulatul lui Becker.
Definiție:
* Sistemul logic cu postulate generale (inclusiv necesitatea și modal modus ponens) și prima dintre cele două afirmații care alcătuiesc postulatul lui Becker este numit S4.
* Sistemul logic cu postulatele generale (inclusiv necesitatea și modal modus ponens) împreună cu ambele afirmații ale postulatului lui Becker este numit S5.
Ferestre către lumile modale
Lumea I: Falsitatea necesară
Sursa: Galeria lui John Spirko. Toate drepturile rezervate.
Frumoasa portretizare a Triunghiului Penrose de către John Spriko ne oferă o fereastră în prima dintre cele patru lumi modale: lumea propozițiilor care sunt în mod necesar false. Ceea ce vedem în această imagine este imposibil din punct de vedere geometric. S-ar putea să doriți să vizitați paginile lui John Spriko pentru a vedea ce crede acesta despre Triunghiul Penrose. Este credința noastră în imposibil doar o limitare în noi înșine, sau este ceva fundamental al naturii realității platonice?
Lumea a II-a: Falsitatea contingentă

Sursa: Galeria lui Slawek Wojtowicz.
Universurile paralele, istoriile alternative și viziunile fantastice constituie toate hrană pentru minte, în a doua dintre cele patru lumi modale: lumea în care propozițiile sunt contingente dar false. Astfel de lumi sunt viziuni a ceea ce este posibil, chiar dacă știm că astfel de lumi nu vor deveni niciodată realitate. În această imagine, vedem portretizarea misterioasă a lui Slawek Wojtowicz a unor corpuri suspendate de "Baby Boomers" plutind în atmosfera superioară a planetei lor.
Lumea a II-a: Adevărul contingent
Sursa: NASA
Lumea adevărului contingent constituie decorul potrivit pentru științe. În vreme ce scriitorii de science fiction pot permite călătorii cu o viteză mai mare decât viteza luminii sau paradoxul bunicului în călătoria în timp, oamenii de știință sunt constrânși de ceea ce este posibil sau de ceea ce este cunoscut. Asta lasă suficient loc pentru aventură.
Lumea a IV-a: Adevărul necesar
Sursa: Baza de date cu imagini fractal de la CNAM. Imagine de Noel Giffin.
Am ales această imagine fractal extraordinară a unui element mandelbrot din cadrul mulțimii mandelbrot drept fereastra către lumea propozițiilor necesar adevărate. Complexitatea infinita a mulțimii mandelbrot ne reamintește atât de eleganța adevărului matematic, cât și de subtilitatea acestuia. În vreme ce unii consideră că lumea matematicii constituie un produs al minții umane, se poate trage concluzia privind mulțimea mandelbrot că poate creația și-a depășit creatorul. Ce minuni rămân a fi descoperite în adâncurile infinite ale acestei mulțimi?
Logica falsă
Deși logica modală poate părea relativ ciudată, în multe aspecte este mai consistentă cu logica vorbirii obișnuite decât este logica prepozițională (calculul prepozițional) folosită de matematicieni. O zonă în care logica modală este utilă este aceea a discutării propozițiilor false. De exemplu, propoziția
Dacă Napoleon ar fi câștigat bătălia de la Waterloo,
atunci limba franceză ar fi înlocuit engleza ca limbaj în cadrul relațiilor internaționale
poate fi dezbătută semnificativ în cadrul logicii modale. Totuși, în logica prepozițională, această propoziție ar fi trivial adevărată, deoarece orice propoziție de forma a b este adevărată în logica prepozițională dacă propoziția a este falsă. Alte propoziții trivial adevărate din logica prepozițională includ
b este adevărată în logica prepozițională dacă propoziția a este falsă. Alte propoziții trivial adevărate din logica prepozițională includ
 b este adevărată în logica prepozițională dacă propoziția a este falsă. Alte propoziții trivial adevărate din logica prepozițională includ
b este adevărată în logica prepozițională dacă propoziția a este falsă. Alte propoziții trivial adevărate din logica prepozițională includ
Dacă Napoleon ar fi câștigat bătălia de la Waterloo,
atunci Statele Unite ar fi devenit în cele din urma o anarhie agrară pașnică
sau
Dacă Imperiul Roman nu ar fi decăzut datorită barbarilor,
atunci computerele ar folosi cifre romane în zilele noastre.
Din nefericire, această propoziție este trivial adevărată în logica prepozițională, la fel ca și
Dacă Imperiul Roman nu ar fi decăzut datorită barbarilor,
atunci computerele nu ar folosi cifre romane în zilele noastre.
Nu par să existe prea multe motive pentru o dezbatere. Să presupunem că r reprezintă propoziția "Imperiul Roman nu a decăzut datorită barbarilor", iar c este propoziția "computerele folosesc numerale romane". Atunci, în logica prepozițională, propozițiile r c și r
c și r ~c sunt amândouă adevărate deoarece r este falsă. Pe de altă parte, în cadrul logicii modale (reflectând mai adecvat vorbirea obișnuită) este rezonabil să se afirme că
~c sunt amândouă adevărate deoarece r este falsă. Pe de altă parte, în cadrul logicii modale (reflectând mai adecvat vorbirea obișnuită) este rezonabil să se afirme că  (r
(r c) este adevărată și
c) este adevărată și  (r
(r ~c) este falsă, sau viceversa. Logicienii modali numesc această formă de implicare deducție pentru a o deosebi de implicația materială așa cum este definită de către operatorul logic
~c) este falsă, sau viceversa. Logicienii modali numesc această formă de implicare deducție pentru a o deosebi de implicația materială așa cum este definită de către operatorul logic  .
.
 c și r
c și r ~c sunt amândouă adevărate deoarece r este falsă. Pe de altă parte, în cadrul logicii modale (reflectând mai adecvat vorbirea obișnuită) este rezonabil să se afirme că
~c sunt amândouă adevărate deoarece r este falsă. Pe de altă parte, în cadrul logicii modale (reflectând mai adecvat vorbirea obișnuită) este rezonabil să se afirme că  (r
(r c) este adevărată și
c) este adevărată și  (r
(r ~c) este falsă, sau viceversa. Logicienii modali numesc această formă de implicare deducție pentru a o deosebi de implicația materială așa cum este definită de către operatorul logic
~c) este falsă, sau viceversa. Logicienii modali numesc această formă de implicare deducție pentru a o deosebi de implicația materială așa cum este definită de către operatorul logic  .
.
Pentru a utiliza falsități într-o argumentare, este important să se distingă diferitele tipuri de necesități modale sau posibilități modale. De exemplu, un argument bazat pe posibilele consecințe ale victoriei lui Napoleon la Waterloo, nu ar trebui să poată presupune că, de asemenea, legile fizicii s-au schimbat. Într-un fel, legile fizicii ar trebui să apară ca fiind mai necesare decât faptul că Napoleon a pierdut bătălia de la Waterloo. În vreme ce asta poate fi puțin îngâmfat din punctul de vedere filozofic, este cu siguranță baza pentru vorbirea obișnuită. În cartea sa, The Nature of Necessity, Alvin Plantinga face diferența între necesitatea naturală pe de o parte și necesitatea logică generală, pe de altă parte. Propoziția
Voltaire a înotat odinioară în Atlantic
este imposibilă din punct de vedere modal al necesității naturale, dar este posibilă din punctul de vedere modal al necesității logice generale.
Pentru modul meu de gândire, este îndoielnic faptul dacă ne putem limita numai la aceste două concepte modale de necesități (sau posibilități). Limbajul și lumea noastră abundă de diverse restricții asupra posibilităților. Știința nu poate ignora logica modală, exilând-o pe tărâmurile speculațiilor metafizice. De exemplu, pentru a înțelege relaționarea cauzală - pentru a afla felul în care un eveniment poate fi o cauza pentru un altul - s-ar părea că trebuie să lucrăm cu falsități în știință. Dacă voi afirma că un anumit medicament provoacă un anumit răspuns la un subiect, atunci s-ar părea că am afirmat că dacă medicamentul este administrat atunci va fi urmat de răspuns, în timp ce dacă medicamentul nu este administrat nu va fi urmat de răspuns. Una dintre cele doua propoziții reprezintă o argumentare falsă.
Proprietăți esențiale

Sursa: Wikipedia. Ilustrație de Thomas Nast - "Merry Old Santa Claus".
Să presupunem că o persoană a pretins că a verificat dacă Moș Crăciun există. Cum am putea confirma asta? Să presupunem că îl întrebăm de ce crede în Moș Crăciun, iar acesta răspunde:
"Păi, am rămas treaz noaptea trecută și am văzut un bărbat în sufrageria mea îmbrăcat într-un costum roșu. Avea un sac mare pe umăr, era destul de gras și avea o barbă albă bogată. Când l-am întrebat cine este, mi-a răspuns: 'Spune-mi Moș Crăciun, amice', și a ieșit apoi pe fereastră."
Ce putem crede despre asta? Putem examina logica adusă în favoarea argumentului pentru existența Moșului, în felul următor:
1. Moș Crăciun este un bărbat gras care poartă un costum rosu și are o barbă albă.
2. Un bărbat gras purtând un costum roșu și având o barbă albă a fost în sufrageria mea noaptea trecută.
Consecința punctelor 1 și 2 este:
3. Moș Crăciun a fost în sufrageria mea noaptea trecută.
4. Dacă Moș Crăciun nu există, atunci nu ar fi fost în sufrageria mea noaptea trecută.
Concluzia punctelor 3 și 4 este:
5. Moș Crăciun există.
În pofida dovezilor consistente din partea a milioane de copii din lumea întreagă, cititorul va fi iertat dacă nu a găsit aceste argumente convingătoare. Mai departe, să presupunem că altcineva care crede de asemenea în Moș Crăciun, furnizează următoarea mărturie:
"Mă găseam în sufrageria mea în ajunul Crăciunului trecut în jurul miezului nopții, și am fost uimit să văd un bărbat care a apărut din șemineu și a intrat în cameră purtând un sac mare pe umăr. Puteam să jur că șemineul nu era suficient de larg pentru a-i permite să pătrundă, dar a reușit cumva s-o facă. Și-a dus degetul arătător de la mâna dreaptă la gură și după un sst!,a scos în liniște din sac un set de lego, un tractor de jucărie și o mașină de spălat adevărată. Cum a reușit să coboare mașina de spălat pe hornul șemineului și cum a încăput în acel sac nu pot să-mi dau seama. Nu era îmbrăcat ca Moș Crăciun: costumul său cafeniu, nu roșu, iar barba era roșie, nu albă. Totuși, avea o licărire în ochi și părea un tip foarte vesel. A dispărut apoi ca prin magie pe horn și a luat câteva prăjituri cu el. Sunt sigur că era Moș Crăciun."
Putem identifica în mod cert o structură logică în acest raționament:
1. Moș Crăciun este un ins vesel și cu puteri magice, care aduce cadouri în ajunul Crăciunului.
2. Un ins vesel și cu puteri magice se afla în sufrageria mea livrând cadouri în ajunul Crăciunului.
Consecința punctelor 1 și 2 este:
3. Moș Crăciun a fost în sufrageria mea în ajunul Crăciunului.
4. Dacă Moș Crăciun nu există, atunci nu ar fi fost în sufrageria mea în ajunul Crăciunului.
Consecința punctelor 3 și 4 este:
5. Moș Crăciun există.
Acum, am putea fi tentați să punem la îndoială veridicitatea mărturiei acestui personaj. Însă, să presupunem pentru moment că amândouă mărturiile prezentate mai sus sunt despre niște evenimente care s-au petrecut în realitate. Este evident că a doua mărturie oferă mai multe motive pentru a crede în Moș Crăciun decât prima. De ce?
Diferența fundamentală între cele două argumentări este reprezentată de definiția lui Moș Crăciun. Dacă Moș Crăciun ar fi definit drept un individ care este gras, are o barbă albă și poartă un costum roșu, atunci în mod clar orice persoană care se potrivește acestei descrieri ar fi, prin definiție, Moș Crăciun. În mod evident există numeroase persoane care se potrivesc acestei descrieri. Așadar, Moșul nu este definit în mod unic prin această descriere. Există și o altă problemă, de asemenea. Dacă Moșul este definit ca fiind o persoană care poartă un costum roșu, atunci acesta încetează să mai fie Moșul atunci când și-l scoate? Ar înceta să mai fie Moșul dacă s-ar bărbieri? Ar deveni altcineva dacă ar ține o dietă și un program de exerciții fizice care l-ar determina să slăbească?
Problema este de o importanță practică. Cunoaștem cu toții persoane care au slăbit ori s-au îngrășat atât de mult, încât prietenii acestora îi recunosc cu greu. Organele de poliție de pretutindeni îi caută pe suspecți în funcție de anumite descrieri și cunosc foarte bine faptul că aceste descrieri nu sunt complet satisfăcătoare drept caracteristici pentru identificare. Care sunt caracteristicile definitorii pentru orice individ? În termeni filozofici formali, cum putem determina dacă un individ este cu adevărat identificat drept "Moș Crăciun" sau este doar cineva care se potrivește descrierii acestuia?
Logicienii modali definesc o proprietate a unui individ ca fiind esențială, dacă este evident faptul că acel individ are acea proprietate. Prin urmare, dacă x este individul cunoscut drept "Moș Crăciun", iar F, este proprietatea de a avea puteri magice, atunci F este o proprietate esențială dacă  Fx este o propoziție adevărată. Altfel, se spune că o proprietate este contingentă. Astfel, a avea puteri magice se pare că reprezintă o proprietate esențială a lui Moș Crăciun, în vreme ce a fi gras, din câte știm, este contingent. Dacă Moș Crăciun există sau nu este irelevant aici. Faptul că Moș Crăciun ar putea sau nu să existe poate fi determinat numai prin deținerea unei informații neechivoce despre proprietățile esențiale ale Moșului, pe care să le putem identifica la acesta, în cazul în care l-am întâlni.
Fx este o propoziție adevărată. Altfel, se spune că o proprietate este contingentă. Astfel, a avea puteri magice se pare că reprezintă o proprietate esențială a lui Moș Crăciun, în vreme ce a fi gras, din câte știm, este contingent. Dacă Moș Crăciun există sau nu este irelevant aici. Faptul că Moș Crăciun ar putea sau nu să existe poate fi determinat numai prin deținerea unei informații neechivoce despre proprietățile esențiale ale Moșului, pe care să le putem identifica la acesta, în cazul în care l-am întâlni.
 Fx este o propoziție adevărată. Altfel, se spune că o proprietate este contingentă. Astfel, a avea puteri magice se pare că reprezintă o proprietate esențială a lui Moș Crăciun, în vreme ce a fi gras, din câte știm, este contingent. Dacă Moș Crăciun există sau nu este irelevant aici. Faptul că Moș Crăciun ar putea sau nu să existe poate fi determinat numai prin deținerea unei informații neechivoce despre proprietățile esențiale ale Moșului, pe care să le putem identifica la acesta, în cazul în care l-am întâlni.
Fx este o propoziție adevărată. Altfel, se spune că o proprietate este contingentă. Astfel, a avea puteri magice se pare că reprezintă o proprietate esențială a lui Moș Crăciun, în vreme ce a fi gras, din câte știm, este contingent. Dacă Moș Crăciun există sau nu este irelevant aici. Faptul că Moș Crăciun ar putea sau nu să existe poate fi determinat numai prin deținerea unei informații neechivoce despre proprietățile esențiale ale Moșului, pe care să le putem identifica la acesta, în cazul în care l-am întâlni.
Un concept adițional de care avem nevoie este cel al esenței unui individ sau obiect. Esența unui individ reprezintă o întărire a noțiunii unei proprietăți esențiale, pentru a o face maximală.
Definiție: o proprietate F reprezintă esența unui individ x dacă pentru fiecare proprietate G, propoziția
 Gx
Gx 
 (Fx
(Fx  Gx) este adevărată.
Gx) este adevărată.
A se remarca faptul că propoziția Fx Fx este o teoremă a logicii prepoziționale. Prin urmare, alături de axioma necesității, avem
Fx este o teoremă a logicii prepoziționale. Prin urmare, alături de axioma necesității, avem  (Fx
(Fx Fx). Așadar, dacă F este o esență a x, putem deduce că
Fx). Așadar, dacă F este o esență a x, putem deduce că  Fx, adică, F este o proprietate esențială a lui x. Bineînțeles, nu fiecare proprietate esențială trebuie să fie o esență.
Fx, adică, F este o proprietate esențială a lui x. Bineînțeles, nu fiecare proprietate esențială trebuie să fie o esență.
 Fx este o teoremă a logicii prepoziționale. Prin urmare, alături de axioma necesității, avem
Fx este o teoremă a logicii prepoziționale. Prin urmare, alături de axioma necesității, avem  (Fx
(Fx Fx). Așadar, dacă F este o esență a x, putem deduce că
Fx). Așadar, dacă F este o esență a x, putem deduce că  Fx, adică, F este o proprietate esențială a lui x. Bineînțeles, nu fiecare proprietate esențială trebuie să fie o esență.
Fx, adică, F este o proprietate esențială a lui x. Bineînțeles, nu fiecare proprietate esențială trebuie să fie o esență.
A sosit momentul să avem în vedere argumentul ontologic original propus pentru prima oară de către Anselm. Însă, asta în partea următoare.
* Traducere și adaptare după "Kurt Gödel's Ontological Argument" de Christopher Small.
©
Toate drepturile rezervate autorului.




Niciun comentariu:
Trimiteți un comentariu